Tree

A tree is a data structure that represents a hierarchical relationship. A link to another node is one way (only from higher to lower, no cyclic connection), and each node has its own subtree.

Component

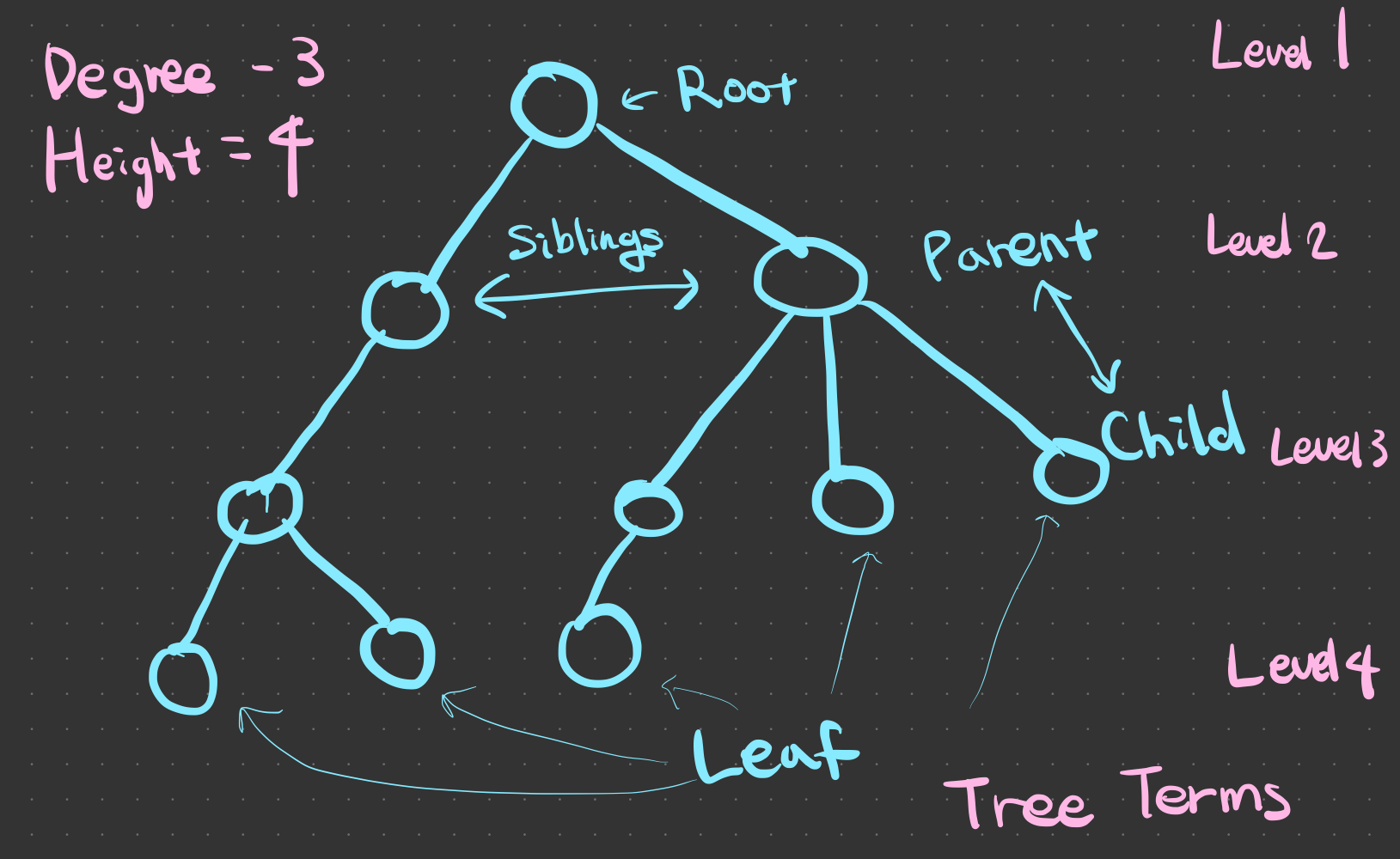
• Node: an element of a tree (data + link to its child node(s))
  • Root node: The top node of a tree
  • Parent node (higher) <-> Child node (lower)
  • Sibling nodes: Nodes that have the same parent nodes.
  • Ancestor node: A parent or higher node
  • Descendent node: A child or lower node
  • Terminal node (=leaf): A node that doesn’t have a child node
  • Internal node: A node that is not a terminal node
• Edge: a line connects two adjacent nodes

Terms

• Level: Depth from the root (level of the root = 1)
• Height (=depth of a tree): The maximum level of a tree
• Degree of a node: Its number of child node(s)
• Degree of a tree: The maximum degree of a node within a tree

Binary tree

A tree whose degree is two or smaller is a binary tree. In a binary tree, every internal node has either one or two children. Every subtree of a binary tree is another binary tree.

N-degree tree can be a binary tree

Every n-degree tree can be transformed into a binary tree by following steps.

1. Remove all edges except the connection between a parent and the most left child.
2. From every node, draw an edge to its sibling at the right.
3. Rotate the tree 90 degrees clockwise.

Variations

• Complete binary tree: All internal nodes have two children nodes
• Perfect/Full binary tree: All level is full (l-th level has 2^l nodes). A perfect binary tree is a complete binary, but not vice versa.
• Skewed binary tree: Every node has either one or zero child.

Traverse

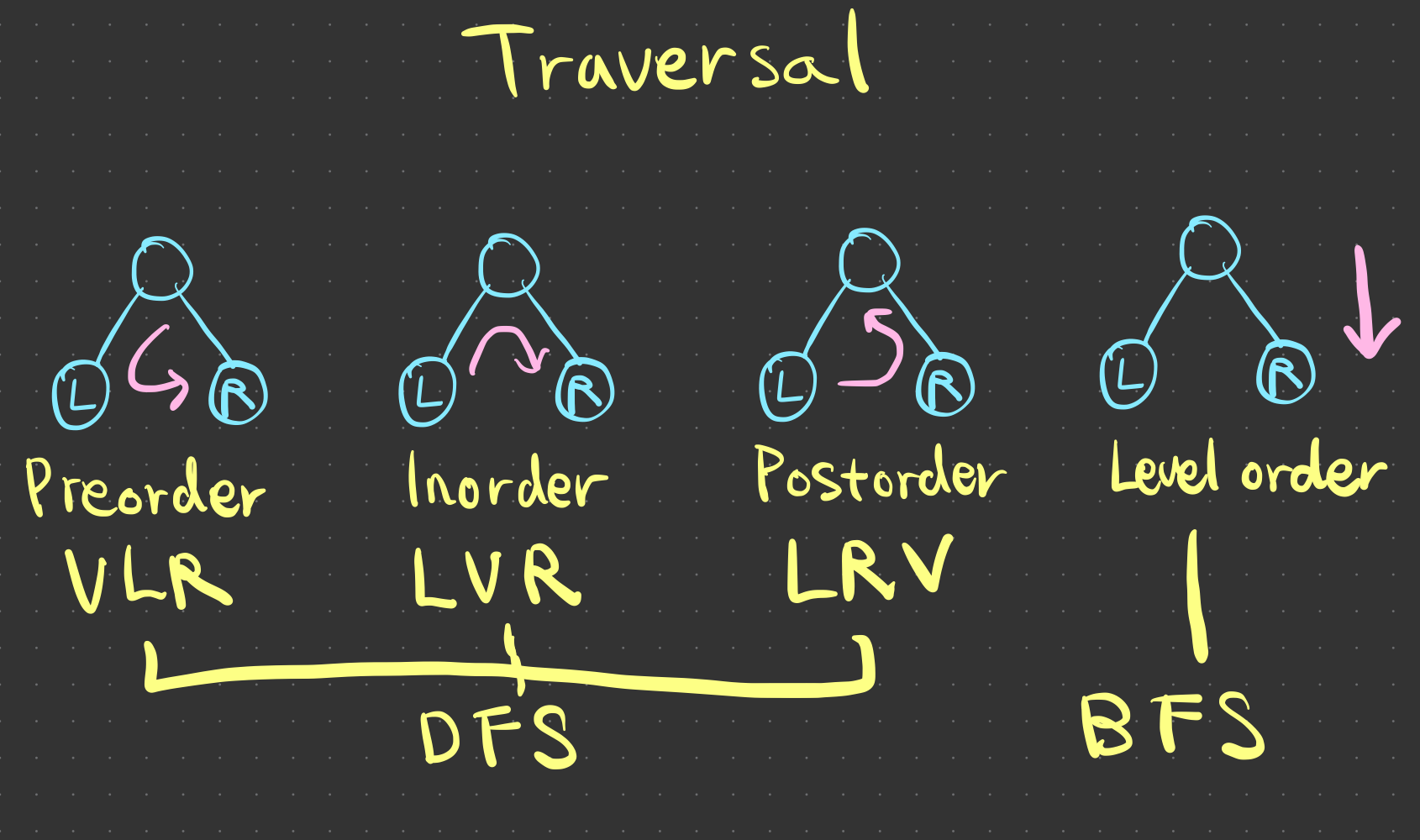
Breadth First Search (BFS)

• Level order traversal: Start from the root, scan all nodes in a level, then move to the next level, and iterate this process.
• Implementation: Queue (children should wait until all of their parent and its sibling(s) is popped out, see the code below)

Depth First Search (DFS)

• Traverse until meeting a leaf, then go back to the previous node, then traverse to another direction, and iterate this process.
• Variation
  • Pre-order traversal: Self->Left child->Right child
  • In-order traversal: Left child->Self->Right child
  • Post-order traversal: Left child->Right child->Self
• Implementation: Recursive algorithm (see the code below) or Stack (The deeper the node, the closer to the top in a stack. Then once the deepest node is searched, it is popped out.)

Implementation

Binary tree implementation can be done using a linked list with two pointers, for its left child and right child.

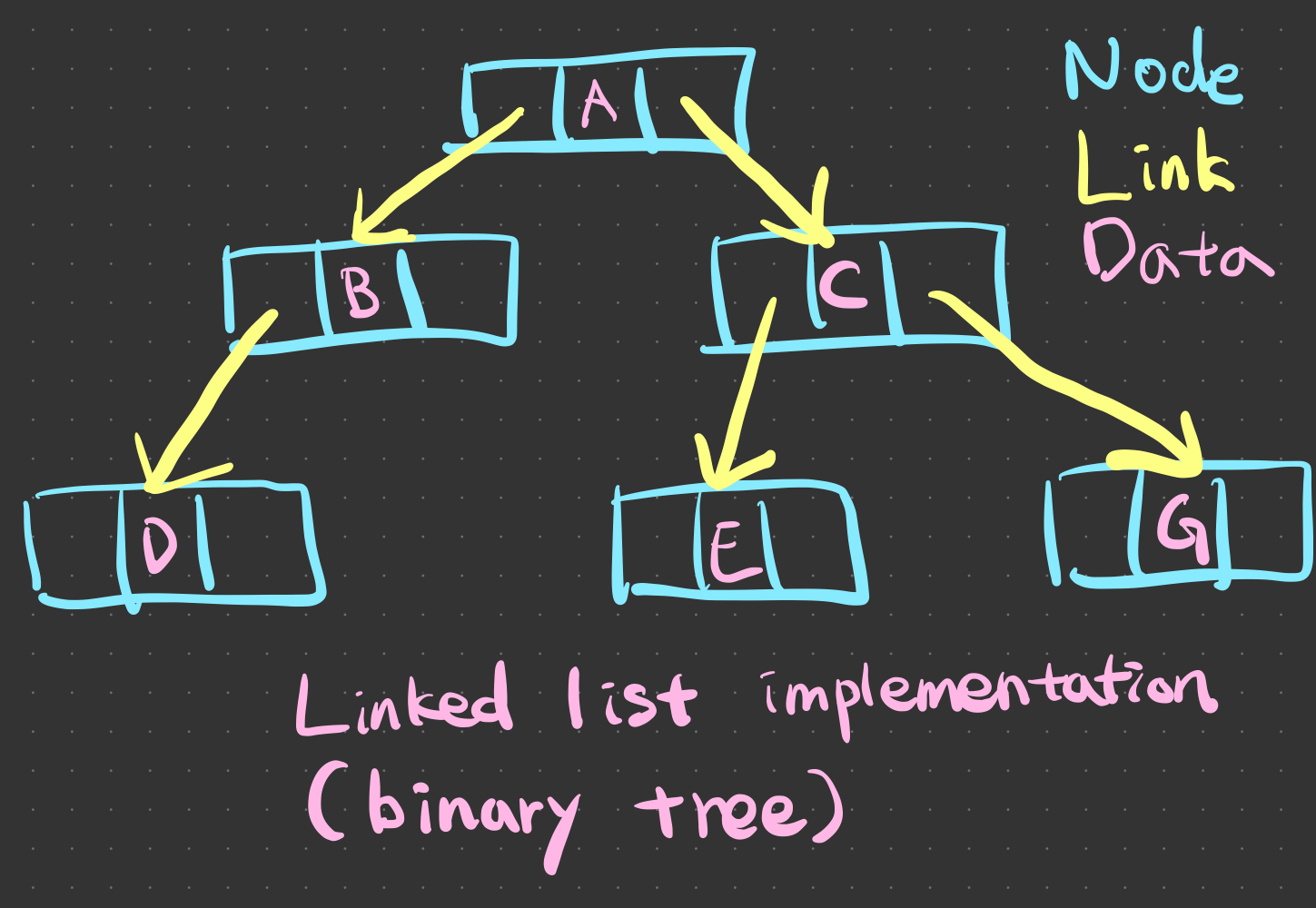
This representation matches the intuitive image of a tree with its node connections. Array can be used as well, however, not efficient in memory usage except for full trees.

from collections import deque 
# can be used as a queue or stack

class Tree:
    class Node:
        def __init__(self, data, left=None, right=None):
            self.data = data 
            self.left = left
            self.right = right
            
    def traverse_level(self,root_node):
        
        if root_node==None:
            return
        
        q = deque()

        # first, add root
        q.append(root_node)
        
        while q:
            
            current_node = q.pop()
            
            print('Level order - node:',current_node.data)
            if current_node.left != None:
                q.appendleft(current_node.left)
            if current_node.right != None:
                q.appendleft(current_node.right)
                
    def traverse_pre(self,root_node):

        if root_node:
            print('Preorder - node:',root_node.data)
            self.traverse_pre(root_node.left)
            self.traverse_pre(root_node.right)
        else:
            return
        
    def traverse_in(self,root_node):

        if root_node:
            self.traverse_in(root_node.left)
            print('Inorder - node:',root_node.data)
            self.traverse_in(root_node.right)
        else:
            return
            

    def traverse_post(self,root_node):

        if root_node:
            self.traverse_post(root_node.left)
            self.traverse_post(root_node.right)
            print('Postorder - node:',root_node.data)
        else:
            return
        


tt = Tree()

node = tt.Node('Root')
node.left = tt.Node('A')
node.right = tt.Node('B')
node.left.left = tt.Node('C')
node.left.right = tt.Node('D')
node.right.left = tt.Node('E')
node.left.left.left = tt.Node('F')
node.left.left.right = tt.Node('G')
node.left.right.left = tt.Node('H')

tt.traverse_level(node)
tt.traverse_pre(node)
tt.traverse_in(node)
tt.traverse_post(node)

Output:

Level order - node: Root
Level order - node: A
Level order - node: B
Level order - node: C
Level order - node: D
Level order - node: E
Level order - node: F
Level order - node: G
Level order - node: H
Preorder - node: Root
Preorder - node: A
Preorder - node: C
Preorder - node: F
Preorder - node: G
Preorder - node: D
Preorder - node: H
Preorder - node: B
Preorder - node: E
Inorder - node: F
Inorder - node: C
Inorder - node: G
Inorder - node: A
Inorder - node: H
Inorder - node: D
Inorder - node: Root
Inorder - node: E
Inorder - node: B
Postorder - node: F
Postorder - node: G
Postorder - node: C
Postorder - node: H
Postorder - node: D
Postorder - node: A
Postorder - node: E
Postorder - node: B
Postorder - node: Root